Rcpp读书笔记:第一章Rcpp简介
1.1 背景:从R到C++
R语言是从S语言进化来的,R和S语言近三十年来一直在进化。举例说明,R语言通过S3和S4类系统实现面向对象特性,也包括新的参考类(reference class)。这种进化,有时候让新手看起来更加复杂(perplexing),也会让中高级开发者感觉语言特性的不连续。巧合的是(Coincidentally),C++也存在同样的问题。
这些争论听起来有些道理,但实际上不是那么回事。人们更加关心语言的可用性。一个语言的关键特性是,可以再现整个数据分析过程。
下边是一个例子,数据来自美国黄石公园老忠实喷泉(Old Faithful Geyser)的喷发和等待时间。喷发时间的密度函数曲线见下图。
xx <- faithful$eruptions
fit <- density(xx)
plot(fit)
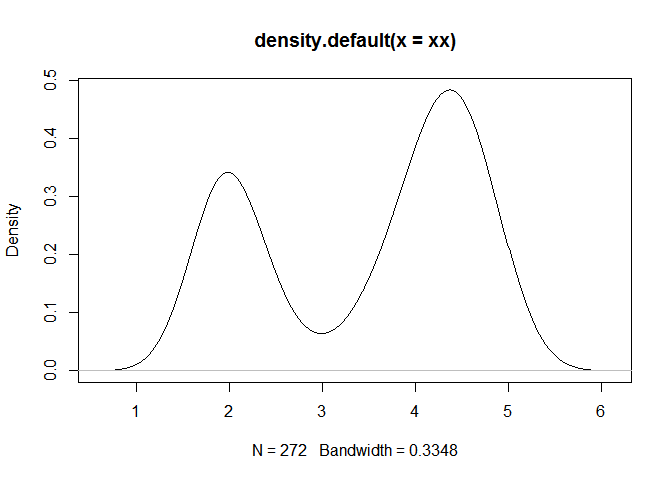
语言完美的展示了R的面向对象特性,利用plot函数,可以直接对函数density的返回结果fit进行图形绘制。
接下来展示的代码,说实话没怎么看懂。
xx <- faithful$eruptions
fit1 <- density(xx)
fit2 <- replicate(10000,
{
x <- sample(xx, replace = TRUE)
density(x, from = min(fit1$x), to = max(fit1$x))$y
})
fit3 <- apply(fit2, 1, quantile, c(0.025, 0.975))
plot(fit1, ylim = range(fit3))
polygon(c(fit1$x, rev(fit1$x)),
c(fit3[1, ], rev(fit3[2, ])),
col = 'grey',
border = F)
lines(fit1)
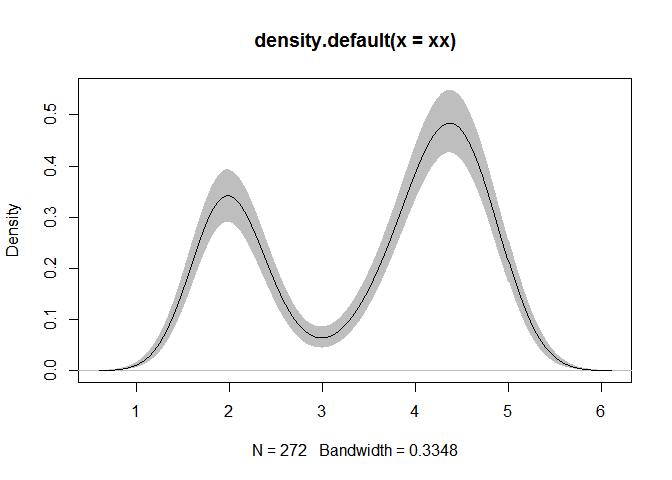
3-6行执行一个最小型的bootstrap抽样。replicate函数对第二个参数重复了10000次。 第二个参数是一个代码段,包含了2个命令。
x <- sample(xx,replace=TRUE);
第一个命令,主要是进行重复抽样,构建一个新的数据集,主要是次序不一样。 第二个命令密度函数。其他就看不下去了,应该要看一下bootstrap的原理才会明白。
R内部执行的关键是它的核心解释器,扩展机制通过C语言执行。C语言的关键特性是可扩展性,通过外部库和外部模块完成。Rcpp的主要优势是,可以替代C,快速的写R的扩展。
1.2 第一个例子
斐波那契(Fibonacci)数列,就是一个递归序列,从第三个数开始,是前两个数的和。公式为:
1.2.1 Fibonacci的R版本
计算函数可以定义为:
fibR <- function(n) {
if(n==0) return(0)
if(n==1) return(1)
return(fibR(n-1)+fibR(n-2))
}
上述函数并没有进行优化,没有对输入值进行判断,也不是特别有效率。譬如输入5,那么会计算fibR(4)和fibR(3),但是等到fibR(4)的时候,会计算fibR(3)和fibR(2),fibR(3)被计算了2次。
1.2.3 Fibonacci的C++版本
令人惊喜的是,可以在Rmd中直接编译、链接和执行C++代码。通过在chunk头中定义engine="Rcpp"或者直接用{Rcpp}表示。
#include <Rcpp.h>
using namespace Rcpp;
// [[Rcpp::export]]
int fibC(const int x) {
if (x == 0 || x == 1) return(x);
return (fibC(x - 1) + fibC(x - 2));
}
上述代码是在R中调用C++代码的一种形式。
对比一下这两个函数的性能,主要是通过microbenchmark包来进行。
library(microbenchmark)
microbenchmark(
fibR(20),
fibC(20)
)
## Unit: microseconds
## expr min lq mean median uq max neval
## fibR(20) 7976.576 8708.070 9308.24655 9045.4980 9653.349 15248.549 100
## fibC(20) 19.231 21.033 35.49196 25.2405 32.752 809.167 100
## cld
## b
## a
从输出结果来看,fibR消耗的时间是fibC的1349 倍。利用Rcpp的性能提升非常大。
1.2.4 Fibonacii的原始调用C++版本
这是调用C++的原始写法,用到了Rcpp的两个关键函数as和wrap。其中as的作用是把SEXP类型的xs变量转换为 C++需要的int类型。SEXP是S expression type的缩写,int是integer的缩写。相反,wrap的作用是把int类型的fib变量转换为R需要的SEXP类型。
int fibonacci(const int x) {
if (x == 0) return(0);
if (x == 1) return(1);
return (fibonacci(x - 1) + fibonacci(x - 2));
}
extern "C" SEXP fibWrapper(SEXP xs) {
int x = Rcpp::as<int>(xs);
int fib = fibonacci(x);
return (Rcpp::wrap(fib));
}
接下来的工作,是要把这两个函数进行编译、链接成一个共享库(shared library),然后在R中载入共享库。这三步,事实上每一步都非常复杂,而且耗时费力。 具体如何做,在第二章中Rcpp的首次编译部分进行了详细阐述,参见链接。 为了简化上述工作,引入inline包,。
1.2.5 Fibonacii的可理解和可执行版本
incltxt <- '
int fibonacci(const int x) {
if (x==0) return(0);
if (x==1) return(1);
return fibonacci(x-1)+fibonacci(x-2);
}'
fibRcpp <- inline::cxxfunction(signature(XS="int"),
plugin = "Rcpp",
incl=incltxt,
body='
int x=Rcpp::as<int>(XS);
return Rcpp::wrap(fibonacci(x));
')
上面的代码,事实上主要是提供了两个参数:
- 第一个参数incltxt包括纯C++代码;
- 第二个参数是包括在函数cxxfunction内的body内容,主要是对接口的定义;
-
cxxfunction的主要目的,是对C++函数进行包装,定义为可以在R内运行;
- XS定义为在R中运行时的输入参数,通过函数signature进一步定义和包装;
- plugin 选择Rcpp来进行接口转换?不确定;
- incl是C++函数体;
- body定义如何转换;
一旦完成上述定义,我们来比较一下三种函数的运行速度,fibR,fibC,fibRcpp。从下边的结果来看,fibC和fibRcpp优势非常明显。
microbenchmark(fibR(20),
fibC(20),
fibRcpp(20))
## Unit: microseconds
## expr min lq mean median uq max
## fibR(20) 8214.248 8578.267 9191.31867 8795.3565 9564.258 15052.943
## fibC(20) 19.230 21.033 28.11543 28.9955 33.653 49.278
## fibRcpp(20) 30.648 32.451 37.19267 36.9580 39.362 94.648
## neval cld
## 100 b
## 100 a
## 100 a
1.2.6 fibonacii第二种解法
这种写法,用到local函数,实际上是local中的代码进行评估,但是local提供一种环境,这些代码中变量仅在这个环境中有效。 计算fibonacii时,对每个数字的fibonacii值存储,下次用的时候直接调用。
mfibR <- local({
memo <- c(1,1,rep(NA,1000))
f <- function(x){
if (x == 0) return(0)
if (x<0) return(NA)
if (x > length(memo))
stop("x too big for implementation")
if (!is.na(memo[x])) return(memo[x])
ans <- f(x-1) + f(x-2)
memo[x] <- ans
ans
}
})
1.2.7 fibonacii第二种写法C++版本
通过1.2.5 的方法,定义如下:
mincltxt <- '
#include <algorithm> //具体的用途?
#include <vector>
#include <stdexcept>
#include <cmath>
#include <iostream>
class Fib {
public:
Fib(unsigned int n = 1000){
memo.resize(n); //设置数组为1000个元素
std::fill(memo.begin(),memo.end(),NAN); //设置数组memo为空值
memo[0] = 0.0;
memo[1] = 1.0;
}
double fibonacci (int x) {
if (x < 0)
return((double) NAN);
if (x >= (int) memo.size())
throw std::range_error(\"x too large for implementation\");
if (! std::isnan(memo[x]))
return(memo[x]);
memo[x] = fibonacci(x-2) + fibonacci(x-1);
return(memo[x]);
}
private:
std::vector <double> memo;
};
'
mfibRcpp <- inline::cxxfunction(signature(xs="int"),
plugin = "Rcpp",
includes = mincltxt,
body = '
int x = Rcpp::as<int>(xs);
Fib f;
return Rcpp::wrap(f.fibonacci(x-1));
')
第一次接触C++类的概念,类Fib包括三个元素
- constructor 构建器或称构建函数,初始化前调用,主要用途是对数组memo进行赋值
- 一个公开的成员函数,用来实现Fibonacci计算
- 一个私有向量memo
貌似必须遵循先公开有私有的顺序?一些特别需要注意的地方:
- 类的定义最后一个大括号后边要加;
- 私有向量,类型的定义,类型要用<>表示。
- 而在代码中,(int) memo.size() 又是用括号表示?
对定义的c++类,在R中进行包装和输出。
比较一下mfibR和mfibRcpp两种方法的效率。
microbenchmark(mfibR(20),mfibRcpp(20))
## Unit: nanoseconds
## expr min lq mean median uq max
## mfibR(20) 42344928 45421139 50029789.07 47745725 52049957 162207493
## mfibRcpp(20) 902 1203 7890.83 2104 13522 47775
## neval cld
## 100 b
## 100 a
从结果看,采用了新的算法,性能进一步提升,R程序的时间大约降低了50%,而C++程序的时间直接下降了一个数量级。注意运行时间,第一种算法单位是microseconds,百万分一秒,而第二种算法是nanoseconds,十亿分之一秒。前者是后者的1万倍。
1.2.8 第三种方法(迭代法)
fibRiter <- function(n) {
first = 0
second = 1
third = 0
for (i in seq_len(n)) {
third = first + second
first = second
second = third
}
return(first)
}
fibRcppiter <- inline::cxxfunction(signature(xs='init'),
plugin = "Rcpp",
body = '
int n = Rcpp::as<int>(xs);
double first = 0;
double second = 1;
double third = 0;
for (int i=0; i<n; i++) {
third = first + second;
first = second;
second = third;
}
return Rcpp::wrap(first);
')
三种方法运行时间的比较:C++代码,迭代法运行时间一次降低。令人惊奇的是,对于R代码,第二种方法的运行时间最长。可能与local函数有关系,第一种方法加载后,第二次不用重新运行?
microbenchmark(fibR(20),
fibC(20),
mfibR(20),
mfibRcpp(20),
fibRiter(20),
fibRcppiter(20)
)
## Unit: nanoseconds
## expr min lq mean median uq
## fibR(20) 7814923 8241440.0 9322281.53 8801816.5 10059133.0
## fibC(20) 18629 22085.5 29771.03 30348.0 34104.0
## mfibR(20) 42768891 46989442.0 50810596.23 49409727.5 53836851.0
## mfibRcpp(20) 902 2704.5 9642.48 10667.0 13371.5
## fibRiter(20) 1202 2104.0 40455.69 6611.0 8413.5
## fibRcppiter(20) 0 601.0 4552.61 3906.5 6911.0
## max neval cld
## 15597095 100 b
## 55888 100 a
## 69434396 100 c
## 19530 100 a
## 3460513 100 a
## 44470 100 a
1.3 第二个例子
关于两个变量1阶自回归(autogressive process of order one for two variables)的描述,公式符号为$VAR(1)$,表述为: 现在考虑更为一般的形式,p阶$VAR(p)$表述为:
1.3.1 R代码
#定义系数矩阵A和残差矩阵u
a <- matrix(c(0.5,0.1,0.1,0.5),nrow = 2)
u <- matrix(rnorm(10000),ncol=2)
rSim <- function(coeff,errors){
simdata <- matrix(0,nrow(errors),ncol(errors))
for (row in 2:nrow(errors)) {
simdata[row,] = coeff %*% simdata[(row-1),]+errors[row,]
}
return(simdata)
}
rData <- rSim(a,u)
上述代码中,需要说明的是coeff是2×2矩阵,而sima[(row-1),]为包括2个元素的向量,二者相乘的结果相当于2×2 %*% 2×1,结果为2×1矩阵。errors[row,]为包括2个元素的向量,跟前边结果相加,相当于2×1 + 2×1。结果是一个2×1矩阵,但是竟然可以作为一个向量赋值给simdata[row,]。
1.3.2 C++代码
本次C++代码用到了另外一个包RcppArmadillo,这个包主要是一个基础的线性代数运算包,包括稠密和稀疏矩阵的四则运算,求逆矩阵等。在本次代码中,主要是用来定义矩阵,以及相关的运算。C++中,矩阵读取的下标是()而不是[]。
suppressMessages(require(inline))
code <- '
arma::mat coeff = Rcpp::as<arma::mat>(a);
arma::mat errors = Rcpp::as<arma::mat>(u);
int m = errors.n_rows;
int n = errors.n_cols;
arma::mat simdata(m,n);
simdata.row(0) = arma::zeros<arma::mat>(1,n);
for (int row=1; row<m; row++) {
simdata.row(row) = simdata.row(row-1)*trans(coeff)+errors.row(row);
}
return Rcpp::wrap(simdata);
'
##创建编译函数
rcppSim <- cxxfunction(signature(a="numeric",u="numeric"),
body=code,
plugin="RcppArmadillo")
rcppData <- rcppSim(a,u)
stopifnot(all.equal(rData, rcppData))
对于simdata.row(0) = arma::zeros<arma::mat>(1,n)不是很理解。
1.3.3 性能比较
boxplot(microbenchmark::microbenchmark(rSim(a,u),rcppSim(a,u)))
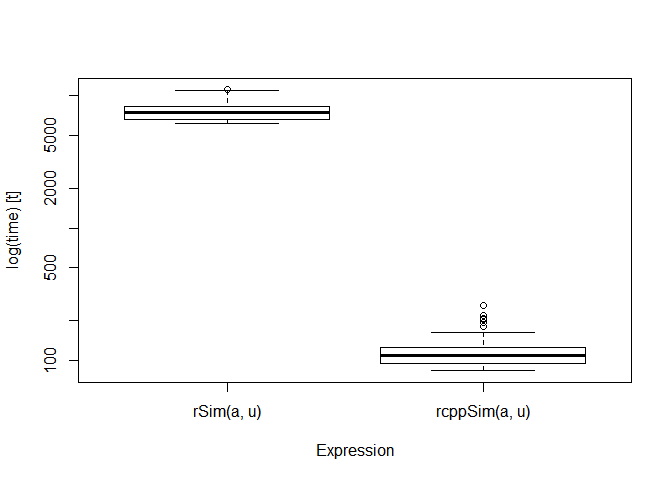
rcppSim比rSim大约快了80倍左右。
- 上一篇 如何可视化家系间的亲缘关系
- 下一篇 线性模型及育种值估计读书笔记1